Jonas Blüthgen Sølvsteen | Bornö 2015 CFD Ocean DSL

Concept

At the Bornö 2015 CFD workshop, the eScience group with Brian Vinter presented a concept for a ocean/climate modelling domain-specific language.

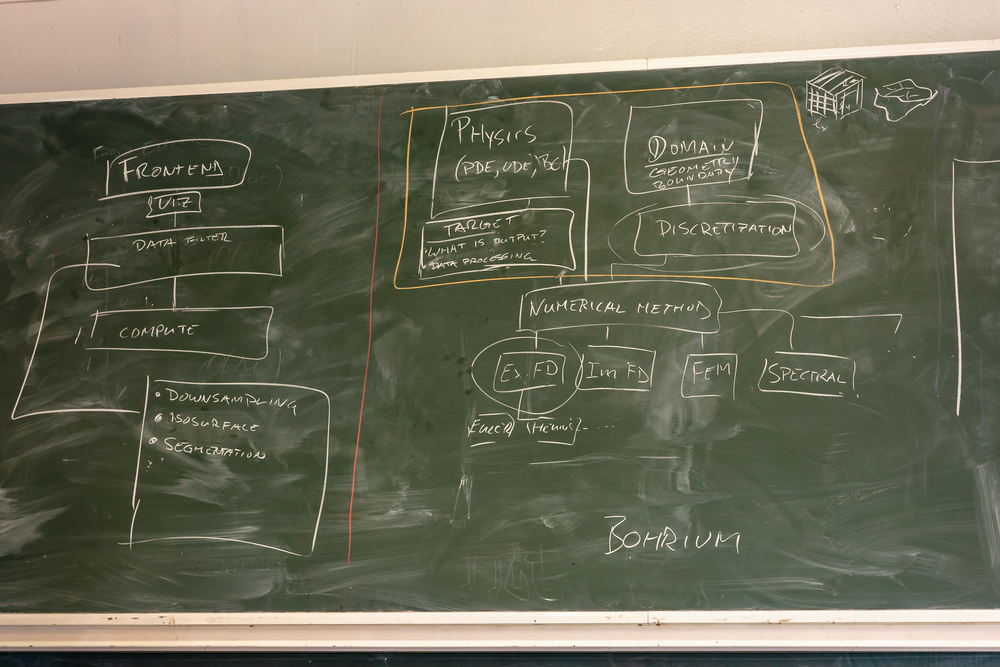
Input

With an ocean model DSL, writing and developing an ocean model requires only these steps:

Define a system of equations for the ocean model (shallow water, ..., primitive equations, ...?) in some high-level conceptual language (to start with, we will use Python instead)
Specify a domain in terms of geometry and boundaries (global/regional ocean or idealized basins with/without topography)
Specify a discretization (unstructured grids, regular grids, ...)
Specify the target: What should be included in the output? Data postprocessing (online/offline)?

Automatized model generation

The system will then automatically

Select the optimal numerical method to solve the equations (although user input can be respected, too)
Generate code for fast execution, using the Bohrium backend, on any infrastructure.

Example Model

Example set of governing equations and boundary conditions for an ocean model (primitive equations)

Prognostic variables

\[u, v, w, \rho, T, S, p\]

Forcings / knowns

\[\rho_0, \alpha, \beta, \kappa, f, g, H, \mathrm{precip}\]

Time derivatives

Momentum equations:

\[u_t + u u_x - fv = \frac1\rho_0 p_x + \kappa u_{xx}\]

\[v_t + u v_x + fu = \frac1\rho_0 p_y + \kappa v_{yy}\]

Temperature and salinity

\[T_t + \vec{u} \nabla \vec{T} = Q\]

\[S_t + \vec{u} \nabla \vec{S} = \mathrm{precip}\]

Diagnostic relations

Pressure

\[p = \int_z^\eta \, \rho \, g \, dz\]

Density

\[\rho = \rho_0 (1 + \beta S - \alpha T)\]

Diffusivity (from mesoscale eddies):

\[K = f(\rho, h, \dots)\]

This could be formulated in various ways, e.g. computed from high-res non-hydrostatic slices (super-parameterization), a coarser run, or another model run

Conservation laws

\[u_x + v_y + w_z = 0\]

Boundary conditions

No normal flow at the boundaries: \(u,v,w = 0\)
Wind stress at the surface: \(\kappa v_z = \tau^y\), \(\kappa u_z = \tau^x\)
Heat/temperature restoring: \(H = (T_1 - T_0) \frac{d}{\lambda_1}\)
Salinity restoring: \(S = (S_1 - S_0) \frac{d}{\lambda_2}\)

Initial conditions

Velocities: E.g. \(u,v,w = 0\) (ocean at rest)
Temperature and salinity: some climatological values (long-term means from obsevations)

Interfaces

Composite systems (e.g. coupled to an atmospheric model)
As additional boundary condition?

Implementation in the DSL

Formulate time derivatives of the prognostic equations

Ocean Model Domain-Specific Language